Linear Transformation

This page was last modified 2010-11-03 10:05:34 by Puchu.Net user Choco. (Show history)

1 Matrix Representation
2 Matrix Multiplication
3 Transforms
4 References

Matrix Representation

While working with libraries like OpenGL, matrices are represented as a 16-element array. There are two representations, row- or column-major and this indicates how elements are stored and manipulated. So if a translation matrix looks like this:

$\mathbf{T}=\left(\begin{array}{cccc} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \\ \end{array}\right)$

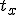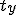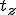For OpenGL, which uses column-major style, elements $t_{x}$ , $t_{y}$ , and $t_{z}$ are accessed with indices 13, 14, and 15. In a system that uses row-major style, these same elements will be accessed with indices 3, 7, and 11. The code fragments below uses column-major style.

[edit]

Matrix Multiplication

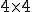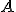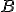Finding matrix product of two $4 \times 4$ matrices $A$ and $B$ involves calculating for each element:

$(AB)_{i,j} = \sum_{k=1}^4 A_{ik}B_{kj}$

In C code this translates to a function like:

void Multiply( const float* A, float* B )
{
  float t[16];

  t[0]  = A[0]  * B[0] + A[1]  * B[4] + A[2]  * B[8]  + A[3]  * B[12];
  t[1]  = A[0]  * B[1] + A[1]  * B[5] + A[2]  * B[9]  + A[3]  * B[13];
  t[2]  = A[0]  * B[2] + A[1]  * B[6] + A[2]  * B[10] + A[3]  * B[14];
  t[3]  = A[0]  * B[3] + A[1]  * B[7] + A[2]  * B[11] + A[3]  * B[15];

  t[4]  = A[4]  * B[0] + A[5]  * B[4] + A[6]  * B[8]  + A[7]  * B[12];
  t[5]  = A[4]  * B[1] + A[5]  * B[5] + A[6]  * B[9]  + A[7]  * B[13];
  t[6]  = A[4]  * B[2] + A[5]  * B[6] + A[6]  * B[10] + A[7]  * B[14];
  t[7]  = A[4]  * B[3] + A[5]  * B[7] + A[6]  * B[11] + A[7]  * B[15];

  t[8]  = A[8]  * B[0] + A[9]  * B[4] + A[10] * B[8]  + A[11] * B[12];
  t[9]  = A[8]  * B[1] + A[9]  * B[5] + A[10] * B[9]  + A[11] * B[13];
  t[10] = A[8]  * B[2] + A[9]  * B[6] + A[10] * B[10] + A[11] * B[14];
  t[11] = A[8]  * B[3] + A[9]  * B[7] + A[10] * B[11] + A[11] * B[15];

  t[12] = A[12] * B[0] + A[13] * B[4] + A[14] * B[8]  + A[15] * B[12];
  t[13] = A[12] * B[1] + A[13] * B[5] + A[14] * B[9]  + A[15] * B[13];
  t[14] = A[12] * B[2] + A[13] * B[6] + A[14] * B[10] + A[15] * B[14];
  t[15] = A[12] * B[3] + A[13] * B[7] + A[14] * B[11] + A[15] * B[15];

  // result overwrites B
  memcpy(B, t, sizeof(float) * 16);
}

[edit]

Transforms

Apply transforms is the same as multiplying with the corresponding transformation matrices.

[edit]

Translate

To move by a translation vector $(t_{x}, t_{y}, t_{z}, 0)$ :

$\mathbf{T}=\left(\begin{array}{cccc} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \\ \end{array}\right)$

[edit]

Scale

To scale by a factor in each axis:

$\mathbf{S}=\left(\begin{array}{cccc} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right)$

[edit]

Rotate

Basic rotations about the x, y, and z axes:

$\mathbf{R_{x}}=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & cos \phi & - sin \phi & 0 \\ 0 & sin \phi & cos \phi & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right)$ rotates the y-axis towards the z-axis

$\mathbf{R_{y}}=\left(\begin{array}{cccc} cos \phi & 0 & sin \phi & 0 \\ 0 & 1 & 0 & 0 \\ - sin \phi & 0 & cos \phi & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right)$ rotates the z-axis towards the x-axis

$\mathbf{R_{z}}=\left(\begin{array}{cccc} cos \phi & - sin \phi & 0 & 0 \\ sin \phi & cos \phi & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right)$ rotates the x-axis towards the y-axis

To rotate 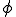$\phi$ radians about an arbitrary, normalized axis $\mathbf{r}$ :

$\mathbf{R}=\left(\begin{array}{cccc} (\mathbf{c}+(1-\mathbf{c})r_{x}^{2}) & ((1-\mathbf{c})r_{x}r_{y}-r_{z}\mathbf{s}) & ((1-\mathbf{c})r_{x}r_{z}+r_{y}\mathbf{s}) & 0 \\ ((1-\mathbf{c})r_{x}r_{y}+r_{z}\mathbf{s}) & (\mathbf{c}+(1-\mathbf{c})r_{y}^{2}) & ((1-\mathbf{c})r_{y}r_{z}+r_{x}\mathbf{s}) & 0 \\ ((1-\mathbf{c})r_{x}r_{z}+r_{y}\mathbf{s}) & ((1-\mathbf{c})r_{y}r_{z}+r_{x}\mathbf{s}) & (\mathbf{c}+(1-\mathbf{c})r_{z}^{2}) & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right) $

where

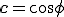
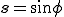
$\mathbf{c} = cos \phi$ and $\mathbf{s} = sin \phi$

[edit]

Shear

To apply shear along x-, y-, or z-axis, modify the coefficients below:

$\mathbf{Sh}=\left(\begin{array}{cccc} 1 & Sh_{xy} & Sh_{xz} & 0 \\ Sh_{yx} & 1 & Sh_{yz} & 0 \\ Sh_{zx} & Sh_{zy} & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right)$

[edit]

References

Akenine-Moller, Tomas and Eric Haines, Real-Time Rendering 2nd Edition, A K Peters: 42-43, 725.

Retrieved from "http://puchu.net/doc/Linear_Transformation"

This material may contain (biased) opinions, inappropriate materials for numerous individuals, work of other authors from the internet, links that refer to other web documents and resources, or origial work that cannot be use for personal or commercial purposes. Please respect the work of original authors.

Categories: Media | Article | Graphic

Contents

Matrix Representation

Matrix Multiplication

Transforms

Translate

Scale

Rotate

Shear

References